IBM’s nye 433-qubit-processor er en vigtig milepæl for virksomhedens køreplan

Fra Arstechnica artiklen:

So, IBM is being careful about not overpromising. "We're not talking about achieving anything like quantum advantage, or anything like that on this device," Chow said. Instead, the qubit count is about assuring people in the field that IBM can continue along its set road map.

Lol. Selv med 433 "qubits" mener de ikke at deres apparat er tæt på quantum advantage overhovedet, hvilket betyder det kan løse opgaver man ikke umiddelbart kan løse med traditionel computing.

Problemet er at jo flere qubits man har gang i, jo mere støj og fejl kommer der også. De 433 qubits kan ikke bare lige aktiveres samtidigt i en beregning og give et brugbart resultat, som jeg forstår det.

Mon ikke der er tale om nogle IBM jakkesæt med bonus KPIer i stil med "mindst 400 qubit" i en chip...

#1

Der er noget vej endnu. Men perspektiverne er ret voldsomme.

De fordobler tilsyneladende antal qubits hvert år. Moores lov genfødt.

Og de bliver vel også mere pålidelige over tid.

Når man når 4000-8000 pålidelige qubits, så vil det have store konsekvenser.

arne_v (2) skrev:

Når man når 4000-8000 pålidelige qubits, så vil det have store konsekvenser.

Man kan vel tage 10 af disse 433 chips og få 4330 "qubits" i dag. Problemet er at få dem til at samarbejde (entanglement) så de kan afsøge et udfaldsrum med pågældende antal bits.

Det virker som om det er meget svært at øge antallet af bits i entanglement, jeg tænker at sværhedsgraden skalerer eksponentielt. Og hvis systemet skal bryde kryptering skal det også tage højde for bit shuffling gennem et betydeligt antal runder, der har hver deres mellem state. Jeg tror ikke kvantecomputere kan blive kryptografisk farlige de næste 50 år, men de skal da nok kunne løse nogle akademiske, ganske irrelevante problemer kun matematikere interesserer sig for.

Kvantecomputere er bare endnu et hype-train ligesom fusionsenergi og batterier bedre end lithium celler :) Men jeg er da klar til at æde den hat, og jeg håber et eller andet sted at jeg tager fejl.

larsp (3) skrev:

arne_v (2) skrev:

Når man når 4000-8000 pålidelige qubits, så vil det have store konsekvenser.

Man kan vel tage 10 af disse 433 chips og få 4330 "qubits" i dag. Problemet er at få dem til at samarbejde (entanglement) så de kan afsøge et udfaldsrum med pågældende antal bits.

Definitionen på en N qubit kvante-computer er vel N qubits som samarbejder.

larsp (3) skrev:

Det virker som om det er meget svært at øge antallet af bits i entanglement, jeg tænker at sværhedsgraden skalerer eksponentielt.

Det er åbenlyst ikke nemt - ellers ville vi have en 8000 qubit kvante-computer idag.

Men udviklingen går stærkt:

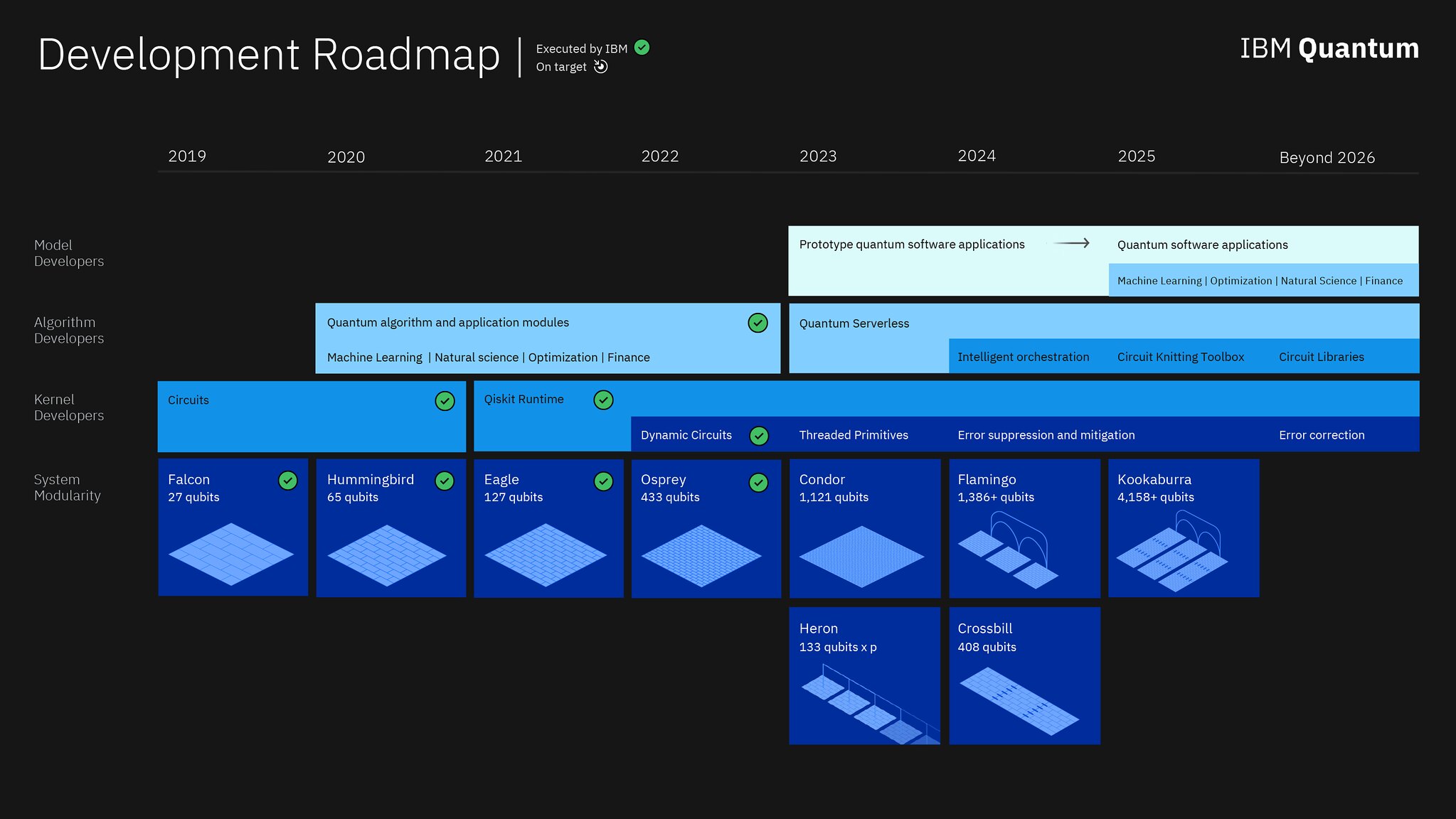
2019 - 27
2020 - 65
2021 - 127
2022 - 433

larsp (3) skrev:

Og hvis systemet skal bryde kryptering skal det også tage højde for bit shuffling gennem et betydeligt antal runder, der har hver deres mellem state.

????

Problemet er vel ikke så meget ved selve krypteringen (AES) med runderne men med key exhange (RSA, DH, EC) og de har ikke runder og er sårbare for kvante-computere.

larsp (3) skrev:

Jeg tror ikke kvantecomputere kan blive kryptografisk farlige de næste 50 år,

Det tror jeg er noget optimistisk.

larsp (3) skrev:

Men jeg er da klar til at æde den hat, og jeg håber et eller andet sted at jeg tager fejl.

Go green. Altså en hat af noget spiseligt.

:-) :-) :-)

arne_v (4) skrev:

Problemet er vel ikke så meget ved selve krypteringen (AES) med runderne men med key exhange (RSA, DH, EC) og de har ikke runder og er sårbare for kvante-computere.

Matematikken ligger over mit niveau.

Men som jeg forstår det vil kvante-computere:
* ændre angreb på AES fra en eksponentiel funktion til en anden eksponentiel funktion via Grovers algoritme
* ændre angreb på RSA/DH/EC fra en eksponentiel/sub-exponentiel funktion til en polynomial funktion via Shors algoritme

Hvilket betyder at AES kan fixes ved at bruge flere bits mens RSA/DH/EC vil være toast.

#3 og #4

Jeg er ikke uenig i at der har været og stadig er meget hype omkring kvante-computere og kryptering.

Der blev snakket om det for 5, 10 og 15 år siden.

Eksempler:

https://newz.dk/nyt-gennembrud-for-kvantecomputere...
https://newz.dk/kvantecomputer-fremvises

:-)

Men der er en stor forskel på kvante-computer hype og XYZ hype.

Med XYZ så kan man fint vente med at gøre noget som helst indtil XYZ faktisk virker.

Med kvante-computer skal man helst gøre noget 25 år inden det virker.

arne_v (4) skrev:

Definitionen på en N qubit kvante-computer er vel N qubits som samarbejder.

Min sarkasme i #1 var grundet i at 433 qubit chippen netop ikke har 433 qubits der kan samarbejde. De har først og fremmest gjort qubits mindre og mindre energihungrende, så der kan presses flere af dem ind i en chip, men:

While the error rates of IBM's qubits have steadily improved, they've still not reached the point where all 433 qubits in Osprey can be used in a single algorithm without a very high probability of error

Since the probability of errors largely scales with qubit counts, adding more qubits to a calculation increases the likelihood that calculations will fail. I've had one executive at a trapped-ion qubit company tell me that it would be trivial for them to trap more ions and have a higher qubit count, but they don't see the point—the increase in errors would make it difficult to complete any calculations. Or, to put it differently, to have a good probability of getting a result from a calculation, you'd have to use fewer qubits than are available.

Osprey doesn't fundamentally change any of that. While the person at IBM didn't directly acknowledge it (and we asked—twice), it's unlikely that any single calculation could use all 433 qubits without encountering an error

arne_v (4) skrev:

????

Problemet er vel ikke så meget ved selve krypteringen (AES) med runderne men med key exhange (RSA, DH, EC) og de har ikke runder og er sårbare for kvante-computere.

Du har ret, Diffie Hellman og RSA har ikke runder og er mere sårbare. Det er simple algoritmer med et enkelt lag af multiplikationer og modulo opfundet i kryptografiens barndom. Jeg kan læse at normal CPU processering allerede i dag kan true RSA, hvis man har nok af det, så disse algoritmer er ved at være passé under alle omstændigheder.

Men kommer kvantecomputere til at overhale CPUer i at true RSA? Lad os se. Jeg har ikke købt stråhatten endnu...

Men key-exchange er noget dynamisk der sker når man sætter en sikker kanal op. Det er ikke så svært igen at opgradere denne process til noget mere robust fremadrettet.

Jeg tænkte mere på eksisterende krypteret materiale med f.eks. AES og SHA hashing der bruges i blockchain. Jeg tror ikke på at kvantecomputere kommer til at kunne kvantemekanisk "gennemskue" 10 runders AES inkl. bit-shuffling, eller 50 runder der bruges i SHA - før vi har fusionsenergi, hoteller på månen, jetpaks og flyvende personbiler som en selvfølgelighed ;)

arne_v (4) skrev:

Go green. Altså en hat af noget spiseligt.

:-) :-) :-)

Måske jeg skulle få den købt alligevel og begynde at lægge den i blød ;)

larsp (7) skrev:

arne_v (4) skrev:

Definitionen på en N qubit kvante-computer er vel N qubits som samarbejder.

Min sarkasme i #1 var grundet i at 433 qubit chippen netop ikke har 433 qubits der kan samarbejde. De har først og fremmest gjort qubits mindre og mindre energihungrende, så der kan presses flere af dem ind i en chip, men:

While the error rates of IBM's qubits have steadily improved, they've still not reached the point where all 433 qubits in Osprey can be used in a single algorithm without a very high probability of error

Det er ikke stabil teknologi endnu.

Men:
- de forbedrer den hele tiden
- konteksten gør at selv høj fejl sandsynlighed kan være et problem

Hvis noget fejler 9999 ud af 10000 gange så vil man normalt kalde det ubrugeligt skrammel.

Hvis en kvante-computer og en dekrypterings opgave fejler 9999 ud af 10000 gange men lykkes 1 gang og et forsøg tager 1 sekund, så er forventet tid for successfuld dekryptering ca. 1.5 time. Helt uacceptabelt.

Success raten skal være meget lavt for at det ikke svækker algoritmen sammenlignet med traditionel computer og brute force.

larsp (7) skrev:

arne_v (4) skrev:

????
Problemet er vel ikke så meget ved selve krypteringen (AES) med runderne men med key exhange (RSA, DH, EC) og de har ikke runder og er sårbare for kvante-computere.

Du har ret, Diffie Hellman og RSA har ikke runder og er mere sårbare. Det er simple algoritmer med et enkelt lag af multiplikationer og modulo opfundet i kryptografiens barndom. Jeg kan læse at normal CPU processering allerede i dag kan true RSA, hvis man har nok af det, så disse algoritmer er ved at være passé under alle omstændigheder.

Det er ikke et alders problem. ECCDH/ECCDSA er nyere end AES.

Det er en forskel på assymmetriske og symmetriske algoritmer. Begge kaldes "kryptering" men det er to helt forskellige problemstillinger. Og de har forskellige løsninger. Med forskellige sårbahed overfor kvante-computere.

larsp (7) skrev:

Men key-exchange er noget dynamisk der sker når man sætter en sikker kanal op. Det er ikke så svært igen at opgradere denne process til noget mere robust fremadrettet.

Det er ikke noget stort problem at opdatere fremadrettet.

Men det er umuligt at opdatere bagudrettet.

Hvilket er kernen i problemet.

larsp (7) skrev:

Jeg tænkte mere på eksisterende krypteret materiale med f.eks. AES og SHA hashing der bruges i blockchain. Jeg tror ikke på at kvantecomputere kommer til at kunne kvantemekanisk "gennemskue" 10 runders AES inkl. bit-shuffling, eller 50 runder der bruges i SHA - før vi har fusionsenergi, hoteller på månen, jetpaks og flyvende personbiler som en selvfølgelighed ;)

Hvis der kan laves en kvante-computer med nok qubits som er stabile, så vil AES kompleksitet ændre sig fra O(2^N) til O(2^(N/2)) eller på almindeligt dansk AES-128 er toast men AES-256 er OK.

NB: Antal runder i AES er forskellig alt efter key size - det er 10, 12 og 14 runder for 128, 192 og 256 bit.

arne_v (9) skrev:

larsp (7) skrev:

arne_v (4) skrev:

????
Problemet er vel ikke så meget ved selve krypteringen (AES) med runderne men med key exhange (RSA, DH, EC) og de har ikke runder og er sårbare for kvante-computere.

Du har ret, Diffie Hellman og RSA har ikke runder og er mere sårbare. Det er simple algoritmer med et enkelt lag af multiplikationer og modulo opfundet i kryptografiens barndom. Jeg kan læse at normal CPU processering allerede i dag kan true RSA, hvis man har nok af det, så disse algoritmer er ved at være passé under alle omstændigheder.

Det er ikke et alders problem. ECCDH/ECCDSA er nyere end AES.

Det er en forskel på assymmetriske og symmetriske algoritmer. Begge kaldes "kryptering" men det er to helt forskellige problemstillinger. Og de har forskellige løsninger. Med forskellige sårbahed overfor kvante-computere.

Og får en god ordens skyld. Bedste brud på RSA med konventionel computer er 829 bit. Og det er ved at være rigtigt mange år siden man skiftede fra 512/1024 bit til 2048/3072/4096 bit, så man bør være OK i.f.t. konventionelle computere.

arne_v (10) skrev:

larsp (7) skrev:

Men key-exchange er noget dynamisk der sker når man sætter en sikker kanal op. Det er ikke så svært igen at opgradere denne process til noget mere robust fremadrettet.

Det er ikke noget stort problem at opdatere fremadrettet.

Men det er umuligt at opdatere bagudrettet.

Hvilket er kernen i problemet.

Jeg må hellere uddybe.

Du skal sende nogle super fortrolige data.

Client og server software (browser og web server eller andet) vælger standarden for den slags som er HTTPS.

HTTPS er HTTP over SSL (TLS).

SSL (TLS) bruger assymetrisk kryptering til at sende en random key og symmetrisk kryptering med den key for data.

Lad os for nemhedens skyld (læs: min dovenskabs skyld) vælge en lidt simplere version end faktisk TLS:
- for assymmetrisk bruges RSA 4096 bit og for symmetrisk bruges AES 256 bit CBC mode
- client genererer en private key og en public key
- client sender public key til server
- server genererer 256 random bit key, krypterer med public key og sender til client
- client dekrypterer random key med private key, AES krypterer data med random key og sender til server
- server dekrypterer data med random key

Dumb hacker opsnakker hele trafikken (public key, random key krypteret med public key, data krypteret med random key). Men det tager 1 milliard computere 1 milliard år at bryde RSA 4096 bit og det tager 1 milliard computere 1 milliard år at bryde AES 256 bit, så det er håbløst.

Smart hacker opsnapper hele trafikken og brænder data på en DVD. Og venter. Efter 5, 10, 15 eller 20 år bliver de nødvendige kvantecomputere tilgængelige og det tager et par sekunder at bryde RSA 4096 bit, så kan random key genskabes og data kan dekrypteres. Og ganske vist er data ikke nyt, men der kunne godt være data som stadig bør være fortroligt efter 5/10/15/20 år.

#8

3 timer - ikke 1.5 time. Men stadig problem.

arne_v (8) skrev:

Hvis noget fejler 9999 ud af 10000 gange så vil man normalt kalde det ubrugeligt skrammel.

Hvis en kvante-computer og en dekrypterings opgave fejler 9999 ud af 10000 gange men lykkes 1 gang og et forsøg tager 1 sekund, så er forventet tid for successfuld dekryptering ca. 1.5 time.

Jeg kan godt se din pointe. Det er trivielt at teste om et resultat er korrekt, og det er exceptionelt svært at gætte den rigtige nøgle. Bare én rigtig, ind imellem, er et gennembrud.

Men spørgsmålet er jo så om vi snakker et par timer eller 100 år selv med en kvantecomputer. Deres executive brugte ordet *any* her:

but they don't see the point—the increase in errors would make it difficult to complete any calculations

arne_v (9) skrev:

Det er ikke et alders problem. ECCDH/ECCDSA er nyere end AES.

Jeg tog for givet at moderne udgaver af key exchange algoritmer ville være meget mere komplicerede end gode gamle Diffie Hellman. Men jeg ser at det er en udfordring at løse dette problem "quantum safe".

Men, jeg har stadig hatte-appetit for bare første gang en kvantecomputer løser f.eks. Diffie Helman, eller lad os bare sige 1024 bit RSA (for at overgå de ~800 bits normale CPUer kunne klare). Jeg har ikke stor tiltro til teknologien. https://www.scientificamerican.com/article/will-qu...

arne_v (11) skrev:

Og får en god ordens skyld. Bedste brud på RSA med konventionel computer er 829 bit. Og det er ved at være rigtigt mange år siden man skiftede fra 512/1024 bit til 2048/3072/4096 bit, så man bør være OK i.f.t. konventionelle computere.

Okay, det er betryggende.

larsp (14) skrev:

Men, jeg har stadig hatte-appetit for bare første gang en kvantecomputer løser f.eks. Diffie Helman, eller lad os bare sige 1024 bit RSA (for at overgå de ~800 bits normale CPUer kunne klare). Jeg har ikke stor tiltro til teknologien. https://www.scientificamerican.com/article/will-qu...

Sandsynligheden for at det sker næste år er praktisk taget nul.

Sandsynligheden for at det sker de næste 5 år er formentligt også meget meget lille.

Men hvad er sandsynligheden for at det sker inden de data der sendes krypteret idag kan offentliggøres uden konsekvenser?

Nogle kinesere hævder nu at kunne bryde 2048 bit RSA med en kvantecomputer.

Men eksperterne tror ikke på dem.

https://www.schneier.com/blog/archives/2023/01/bre...

https://scottaaronson.blog/?p=6957

https://www.linkedin.com/posts/sergiogh_are-rsa-cr...

Men:

https://techmonitor.ai/hardware/quantum/who-are-ea...